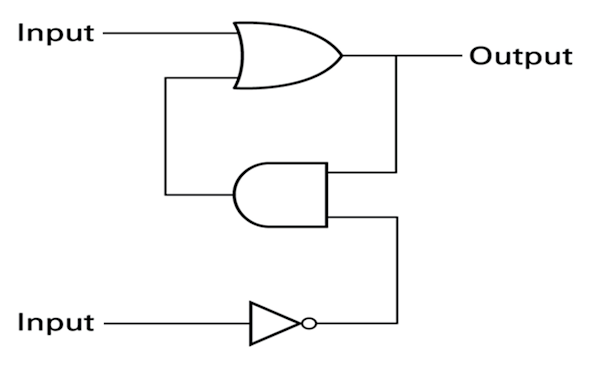
[計算機概論] float-point
先找一篇別人寫好的,這樣就不用從頭到尾都自己寫筆記(欸): 從 IEEE 754 標準來看為什麼浮點誤差是無法避免的 (以下代稱為「該文」) 看過 于天立教授的計算機概論單元 2 之後,我對該文的補充筆記: 「超127 格式」是怎麼回事 exponent 的部分,採用的是 Excess 的定義方式(可參考 定義負數 ),所以,要把十進位的數字 n ,轉成定義中對應的 bits 時,要先把 n 加上某個微調的值,然後轉成二進位,才會得到定義中對應的 bits。如何取得微調的值?看 exponent 有幾個 bits,例如說是 k bits,那麼那個微調的值,就是 2 k-1 -1。該文中的單精度浮點數,exponent 是 8 bits,所以微調的值是 2 8-1 -1 = 127。 不過,真的完全按照 定義負數 中的說法的話,那個微調的值應該是 2 k-1 才對。我目前的判斷是,這個 -1 的誤差,可能是來自於兩者的「哪組 bits 對應到哪個數字」的定義表,有一點點出入,但規律是沒有變的。 fraction 為什麼要去掉 1 正規化後,數字的格式(先不考慮 0 這個數字)固定會長成 n * 2 m 這個樣子,其中 1 ≤ n < 2。既然正規化後,所有數字都一定是 1.XXX * 2 m 這個長相,那麼整數部分的 1 乾脆就不要存起來,這樣省下來的記憶體空間,還可以拿來做更有效的運用。那麼,要怎麼表示 0 呢?所有 bits 都是 0 的話,就代表是 0。如果把「全部都是 0 的 bits」,依照 sign、exponent 跟 fraction 的規則是解讀的話,以單精度浮點數為例,我猜,得到的數字是 2 -128 (或者是 -126 次方?因為 IEEE-754 Floating Point Converter 在 exponent 都是零的時候,顯示的是 -126 次方),總之就會是這個正規化所能代表的最小的正數。但因為要把這個全部是 0 的 bits 改成拿來表示 0,所以「這個正規化所能代表的最小的正數」就被犧牲,變成無法被表示了。 其他 知道浮點數的表示方式後,就可以計算出這個表示方法中,「比 0 大的數字中最小的那個數字(我猜,應該是:sign 是 0,exponent 全部是 0,fraction 只有最後一...